Skip to content

Rowan’s OBC Method for 2x2x2x2

Rowan developed this method for Orienting Both Cells while trying to solve the physical 2x2x2x2 for the first time in a YouTube video.

Steps

Inspection

Before starting the solve, inspect the puzzle for an opposite colour pair that has 4 or fewer stickers oriented to the Left/Right axis (x-axis). They can be made of any colour in the colour pair, and can be in any spot on the puzzle.

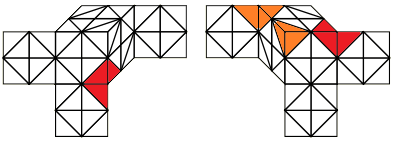
4 or less on 2×2×2×2

4 red/orange corners oriented to L/R

Getting 8 Oriented to Y-axis

Hold the puzzle vertically, and use block building to orient 8 pieces on a cell to the y-axis using the same colour pair that has 4 or less from inspection. This step is intuitive and does not require any RKT.

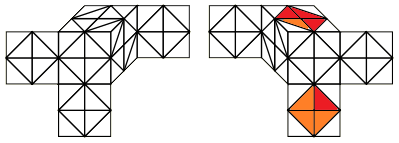
8 to y on 2×2×2×2

8 red/orange corners oriented to U/D

Getting 12 Oriented to Y-axis

Now use RKT to orient a layer of 4 stickers on the other cell, leaving you with a “last layer” of 4 unoriented pieces on one of the cells.

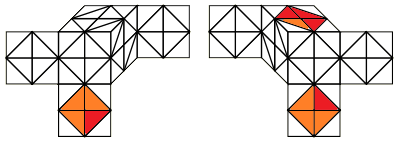
12 to y on 2×2×2×2

12 red/orange corners oriented to U/D

Fixing the Last Layer

Gyro the puzzle such that the 12 pieces that were oriented end up on the x-axis. Now you should have 4 (or fewer) stickers from that colour pair oriented in other directions besides the x-axis. All you need to do is use RKT to make it into a layer that looks like a possible OCLL case, not worrying about messing up the other 12 corners.

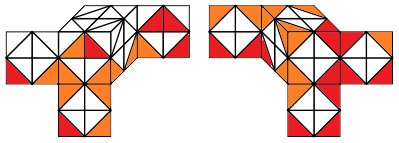
H case on 2×2×2×2

an H OCLL case set up on LU

From here, gyro back. Now you will have a normal OCLL case that you can solve using RKT. After doing that algorithm, you should have all 16 corners oriented to the y-axis. Finally, you just gyro to put them all on the x-axis, and OBC is solved.

Analysis

This technique takes more moves than other known OBC methods, and it uses up to 4 gyros. Besides the skip case where everything is already oriented, the best possible case for this technique uses 3 gyros, making it slower than other techniques. It also requires knowing the OCLL algorithms, which other techniques don’t.