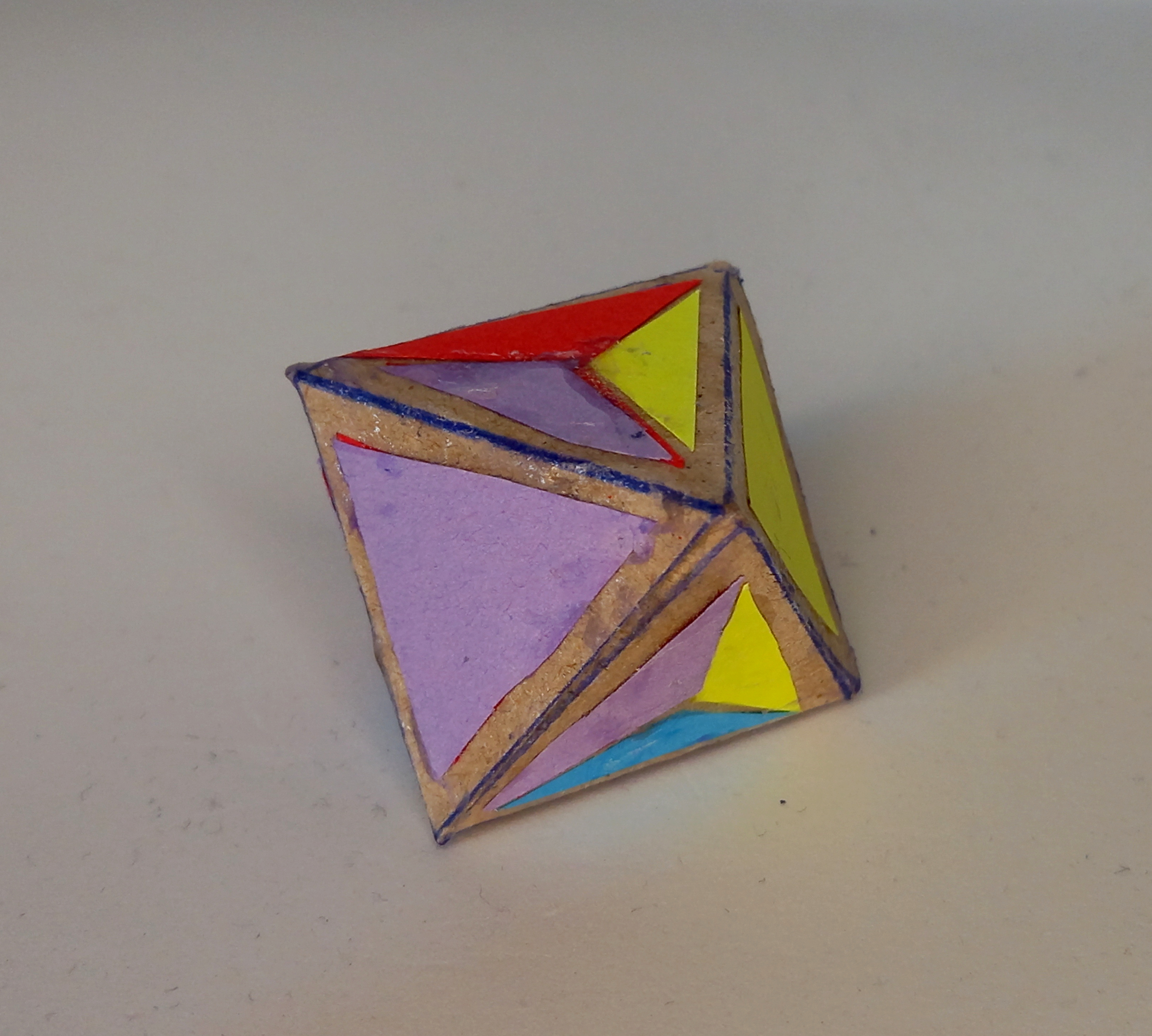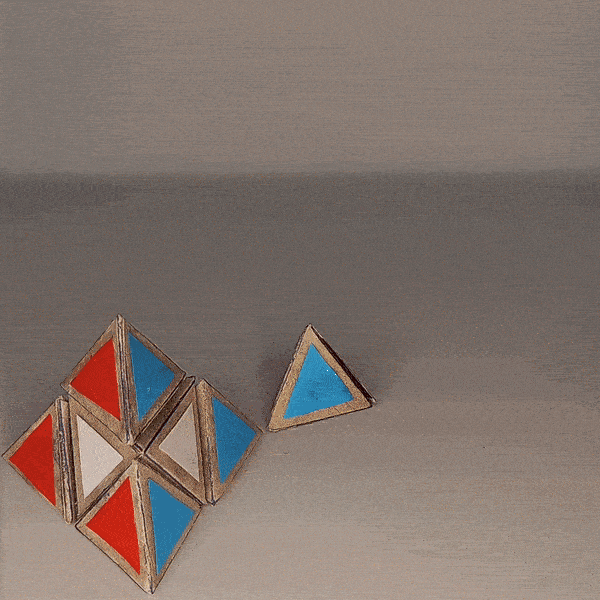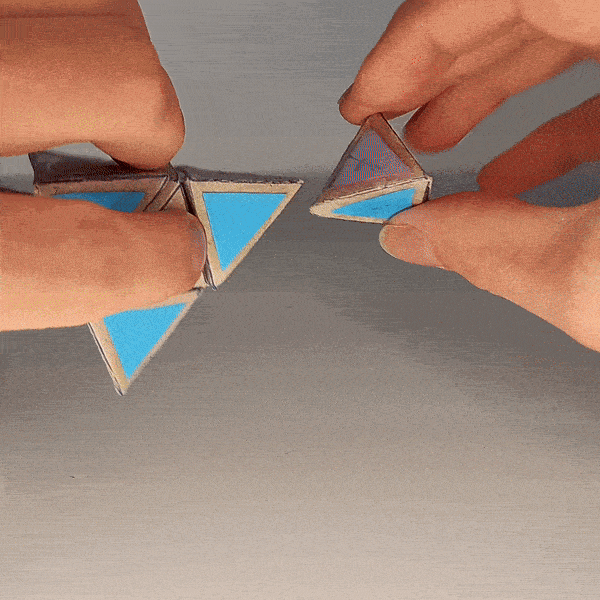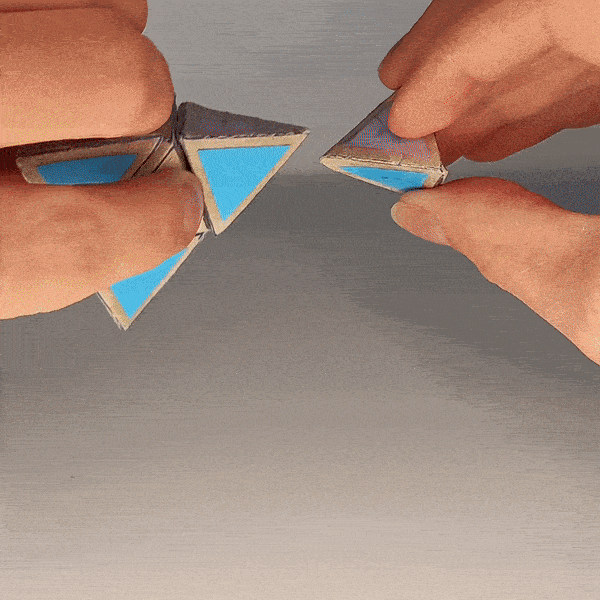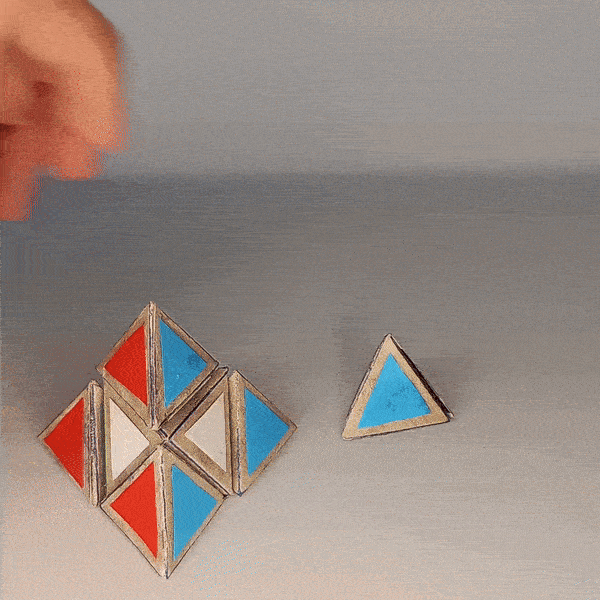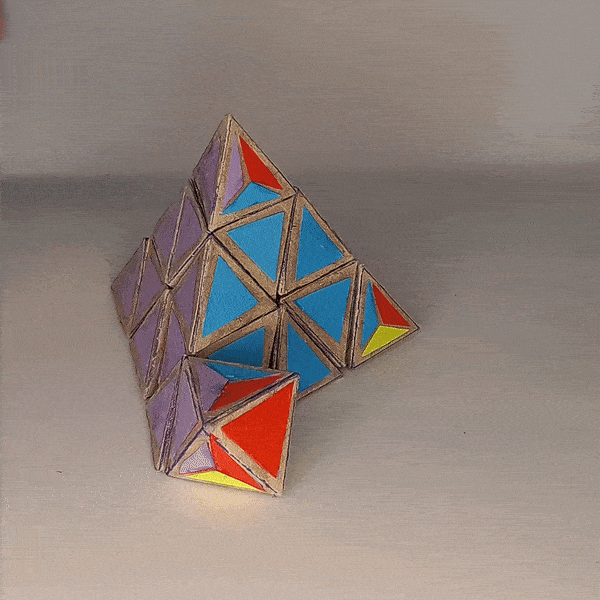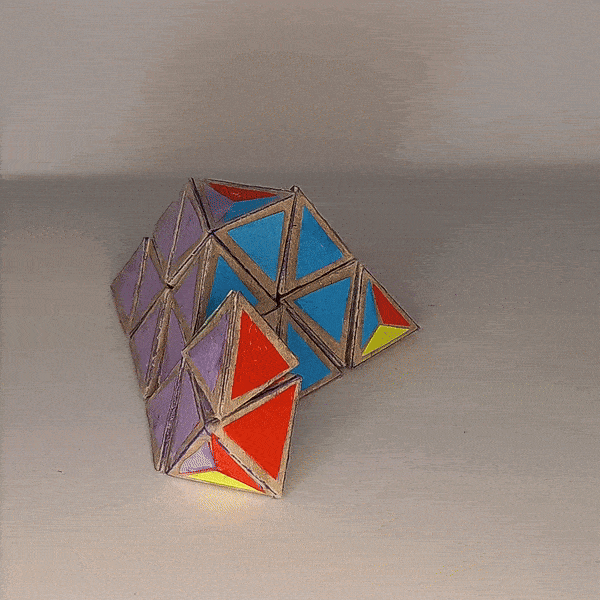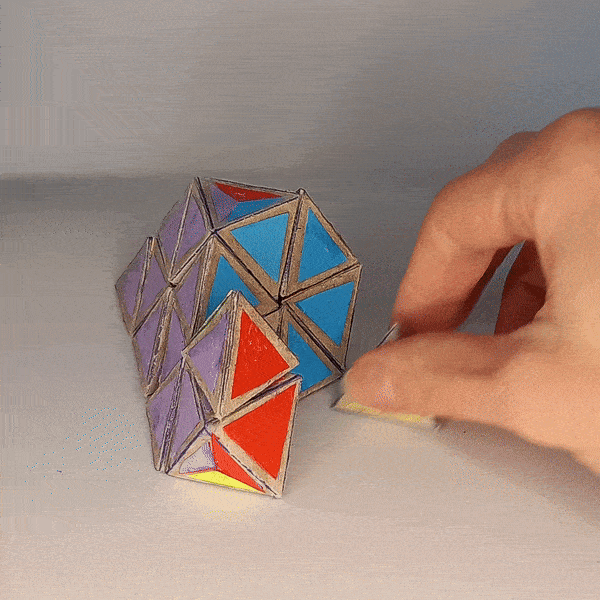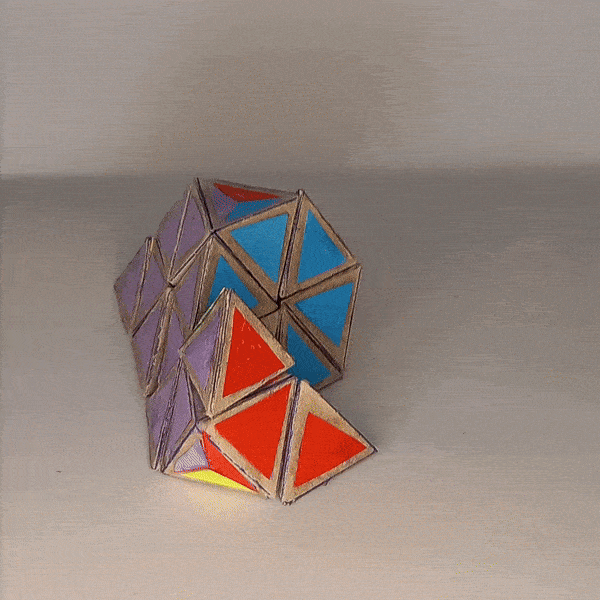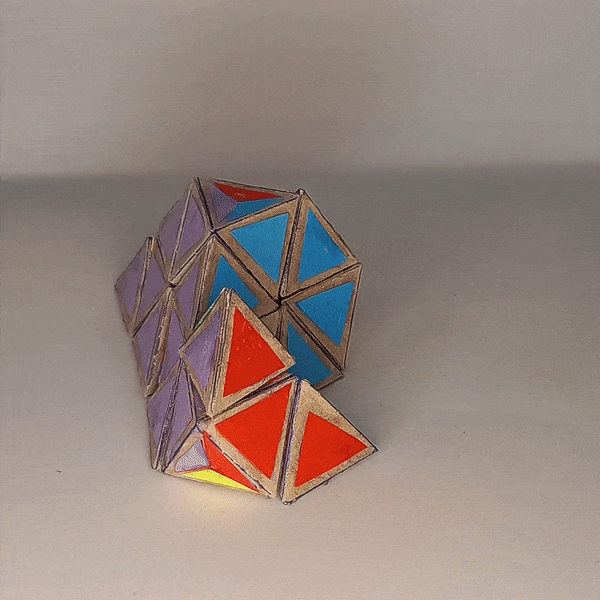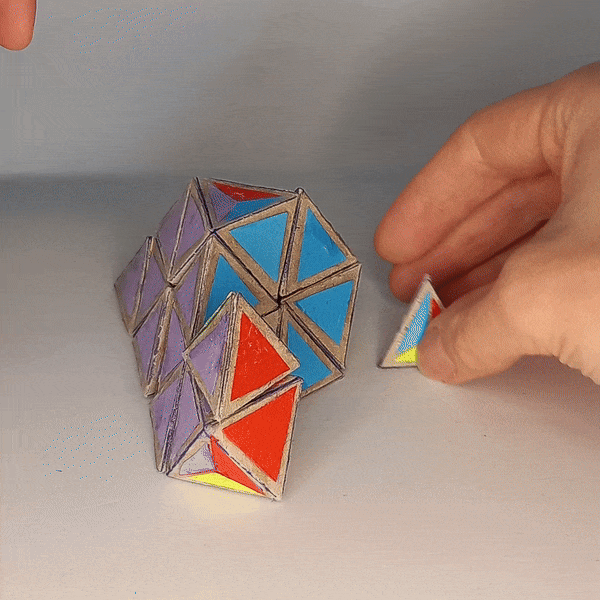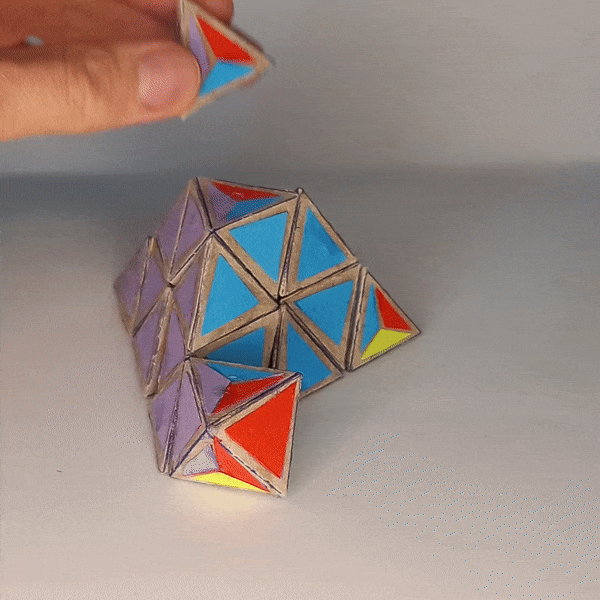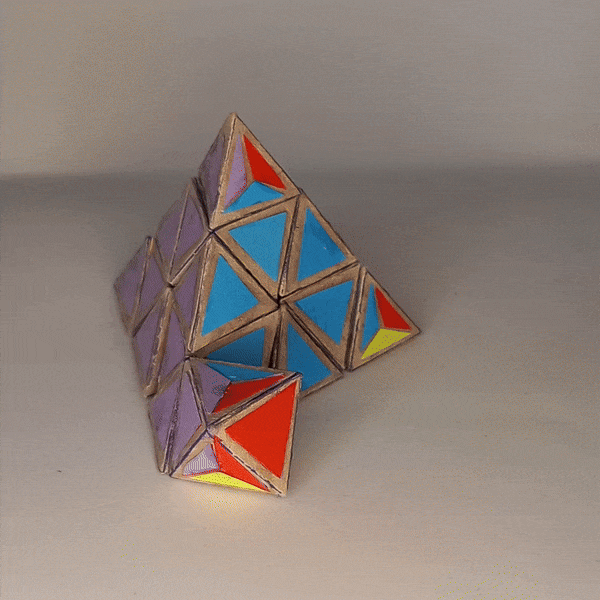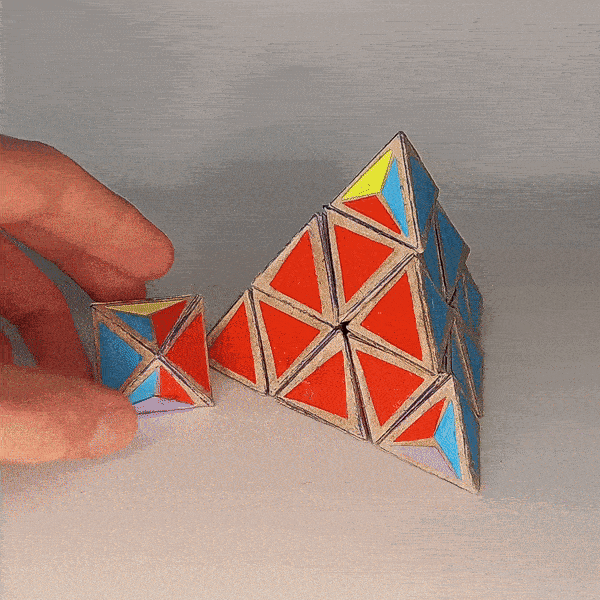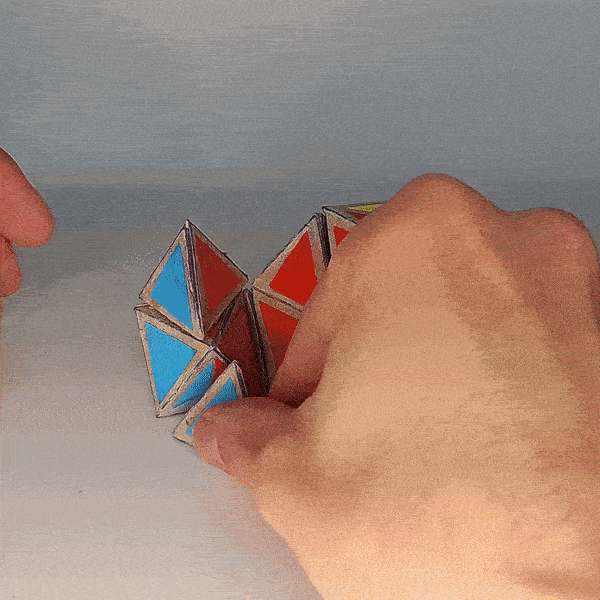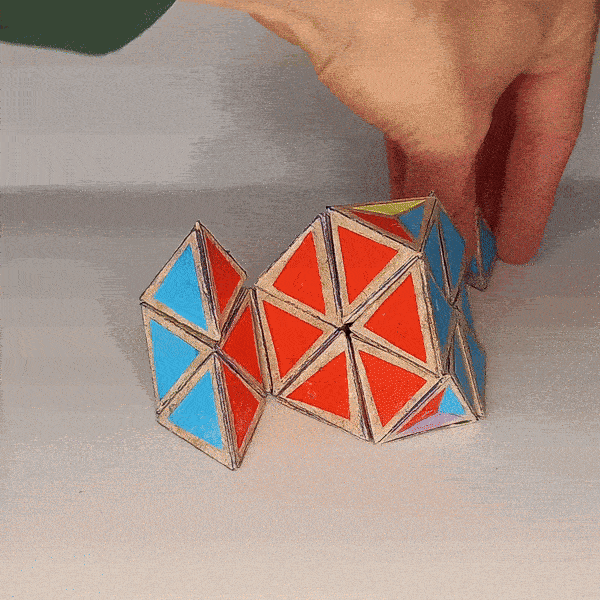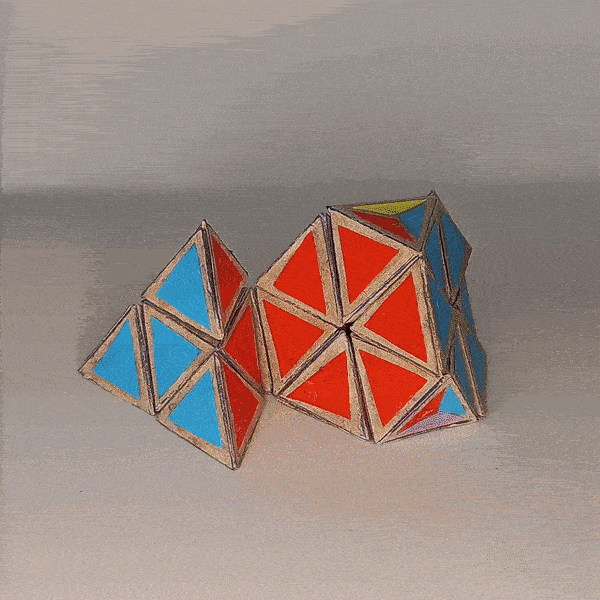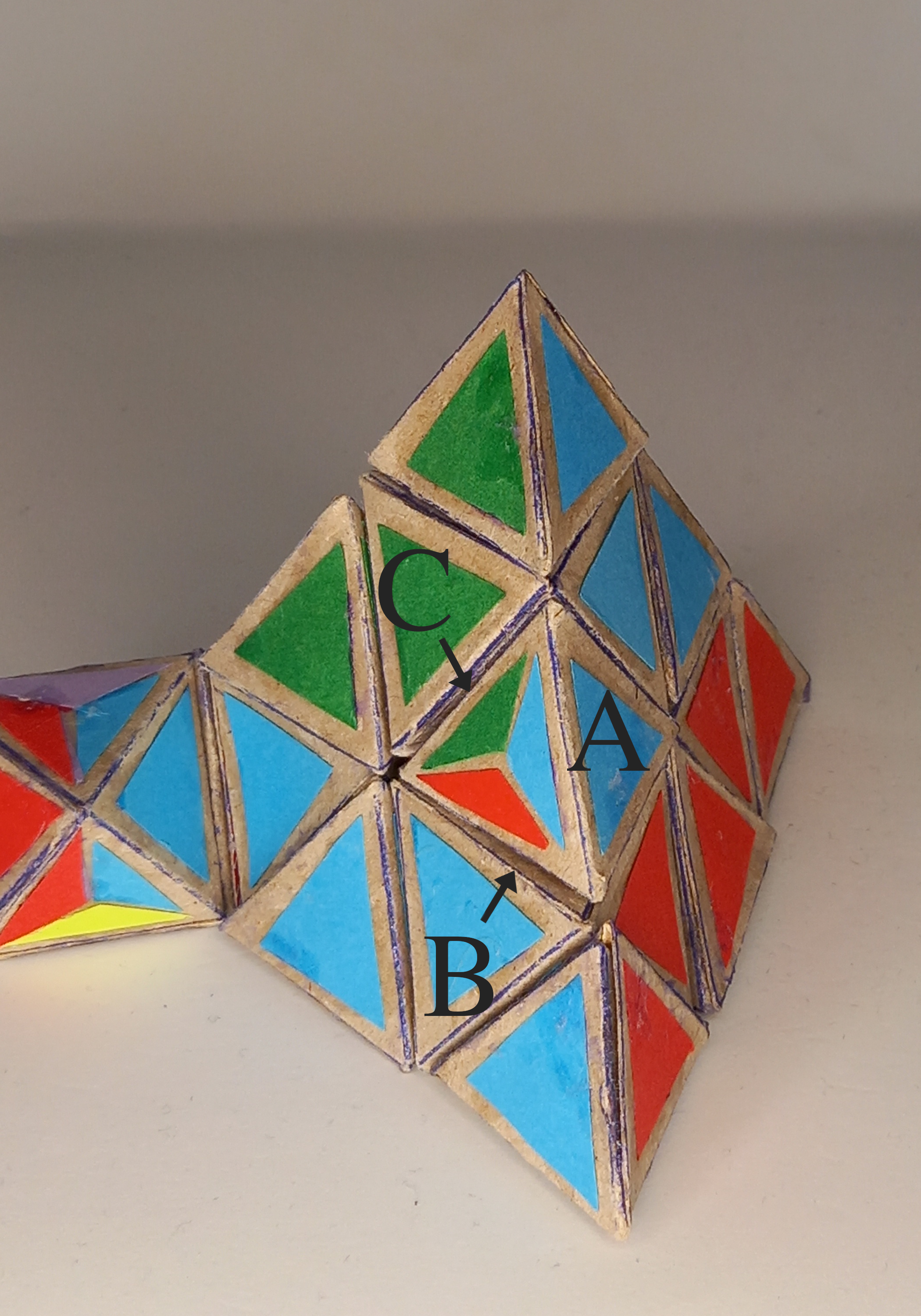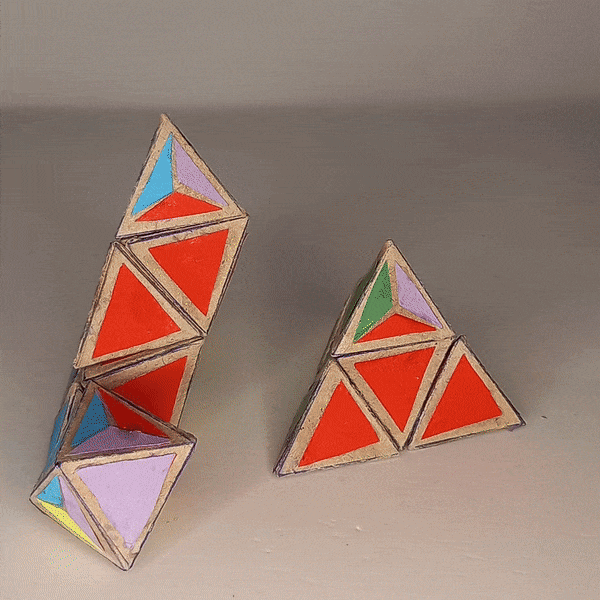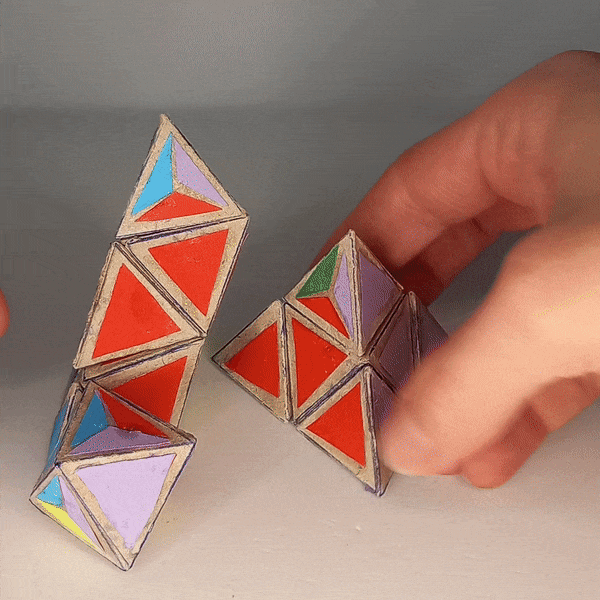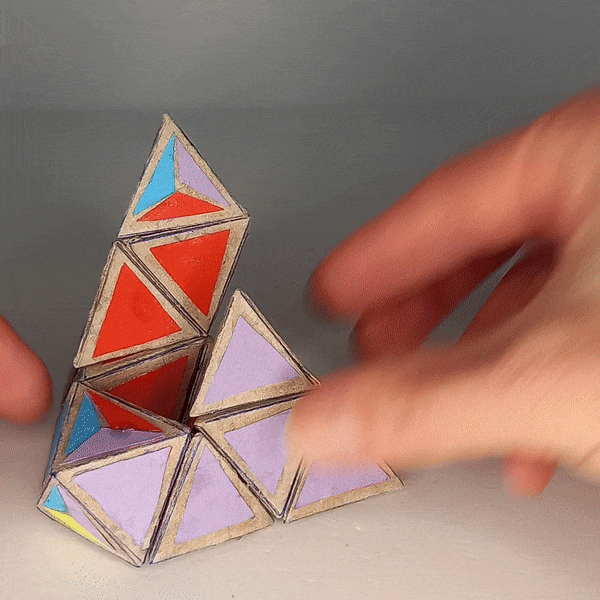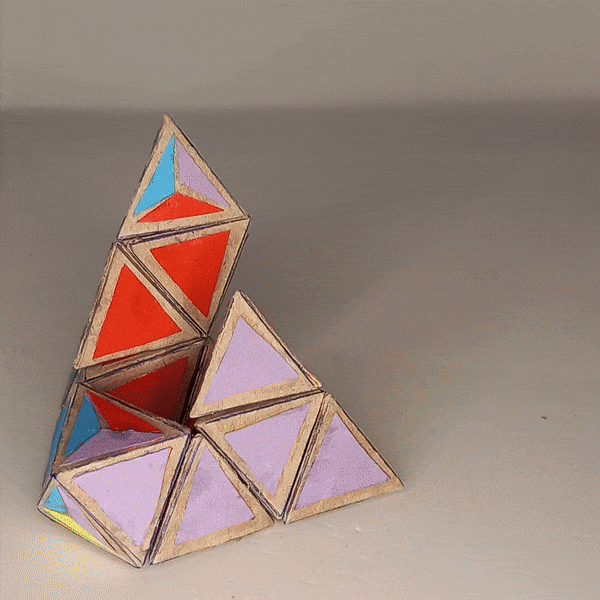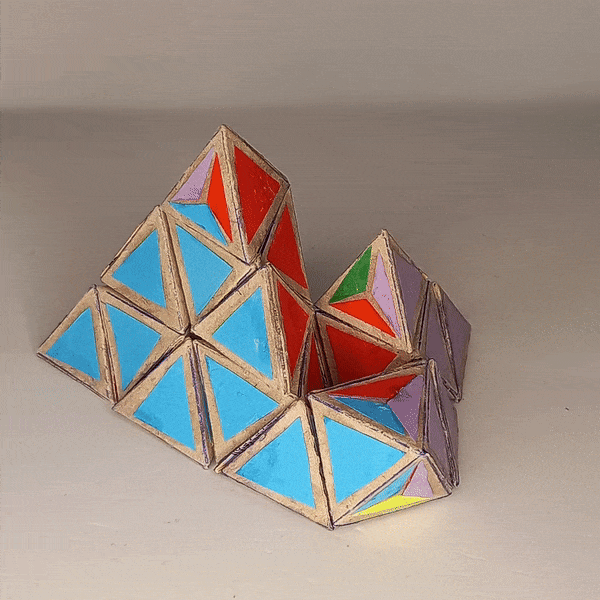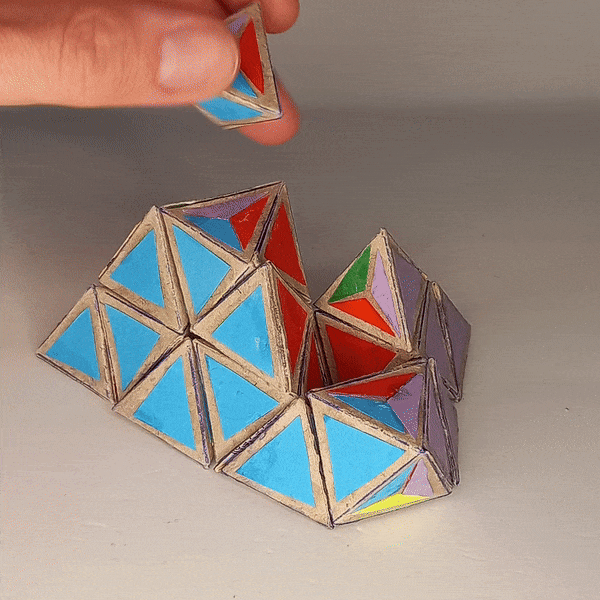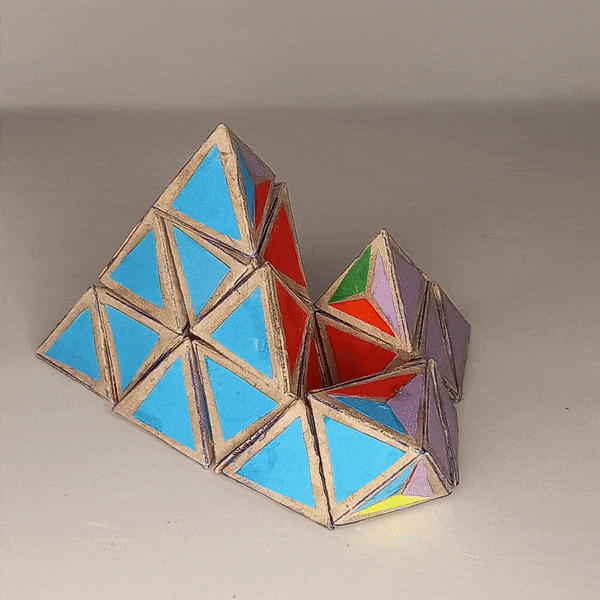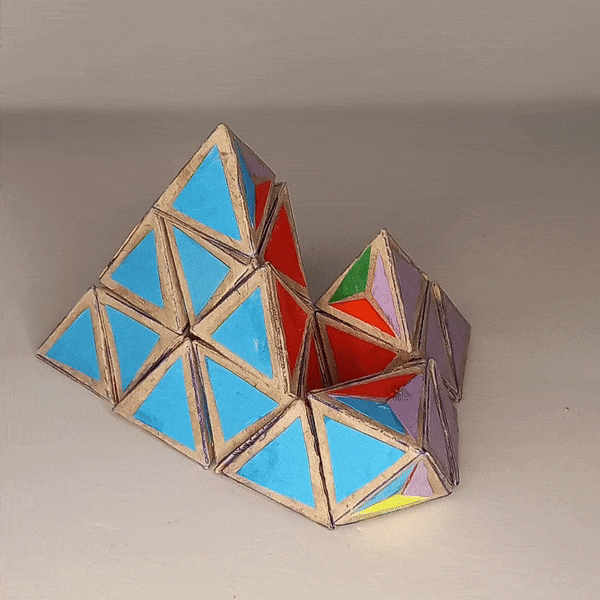Dominik’s 4D Pyraminx

Dominik’s 4D Pyraminx

4D Shape: 5-cell

Physical Shape: Tetrahedron + small Octahedron

Pieces: 5 4c, 10 3c

Magnets: 180 Completed: 2023 Dec 28

Introduction

History

Based on some ideas for the 4D pyraminx, Dominik first created a paper model in mid-December of 2023. After some suggestions from Melinda Green he created the prototype with magnets which was the first functioning version of this design. In April 2024 he finished an improved 3d printed version of the puzzle.

How does it work?

The puzzle can be moved like a pyraminx but with some additional legal moves. The edges that are in the position of the trivial tips can’t legally be twisted.

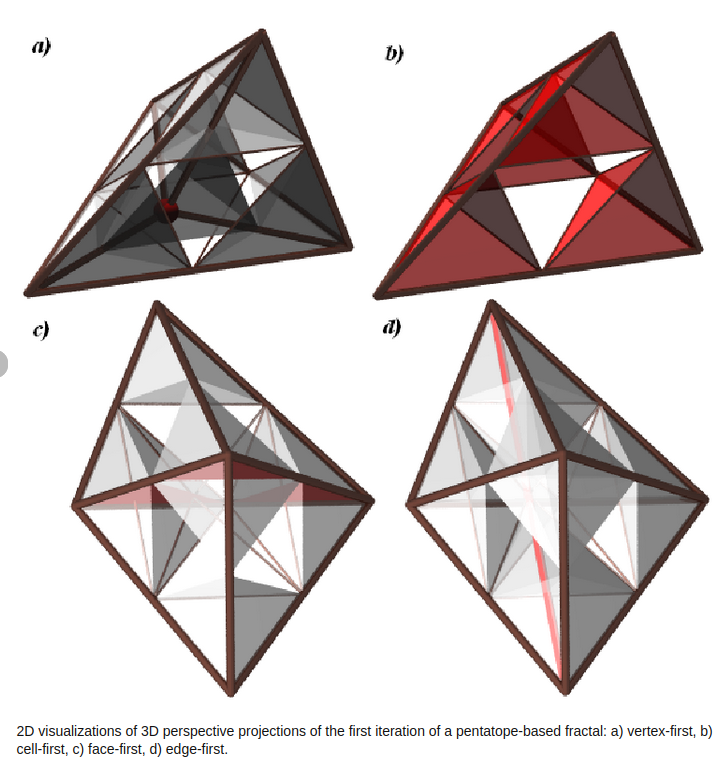
There are a few ways to project a 5-cell into 3d space. In a vertex-first projection the “hidden” cell is on the “outside” of the others while in a cell-first projection it is on the “inside”. My design for the 4D pyraminx represents the latter way. In a solved state we have 4 colors on the outside and one on the inside of the puzzle.

2D visualizations of 3D perspective projections of the first iteration of a pentatope-based fractal: a) vertex-first, b) cell-first, c) face-first, d) edge-first.

(pictures: projections Source, vertex first pyraminx, cell first pyraminx Source)

The Pieces

There are ten tetrahedron-shaped 3-colored edge pieces where the fourth face is split into three colors.

Then there are five octahedron-shaped 4-colored center pieces where four of the faces are split into three colors of the adjacent faces.

The five 4-colored trivial tips can also be represented by tetrahedrons but with the current design they would need to be a separate arrangement. So this puzzle without the trivial tips represents just the truncated pyramnix.

Chirality

For the pieces to fit together in the correct color arrangement they need to have the same chirality. There is a left-handed and a right-handed version of the pieces and the centers and trivial tips need to have the same order of colors. Since the edges are allowed to be in more states the chirality doesn’t matter as much but if the chiralities don’t line up one color will be “favored” in a certain orientation.

Moves

There are some legal moves that don’t represent a movement in the 4D puzzle.

Edge Migration

You can move edges to a corresponding position on the “free center” and back.

Reorient Edges

Edges can be in two states in relation to a center. They can align with the split face towards the center which will be call a “correct” state or the split face can be away from the center which will be called an “incorrect” state. In the latter case the edge can legally be oriented in three different ways.

Next we have moves which do represent a movement in the 4D puzzle. Unlike the normal 3D pyraminx the tips can’t legally be twisted. Other than that the four different moves of turning two layers of the pyraminx is legal. In the 4D version of the puzzle we have 20 different of such slice moves. Here are the four axes of rotations that are allowed for each 2-layered pyramid.

If you perform such a move on each of the four sides of the tetrahedron you get a total of 16 moves. For the missing four moves we can “equip” the free octahedron with the edges by swapping them onto it and perform the rest of the rotations that way.

After the rotation you have can move the edges back.

…

This is not necessary for a solve, though, since you have access to all the edge pieces through the 16 other moves.

Legal States

To keep the puzzle in a legal state sometimes after certain rotations we need to make edge reorientations. When performing a non-standard slice move an edge that isn’t in a correct state regarding the center that has rotated can after a turn show a split face.

If it isn’t in a tip position it needs to be reoriented for otherwise the puzzle can get into an illegal or impossible state and also the color alignment becomes unknown for practical purposes when the puzzle is scrambled.

How does this work? Before the rotation the colors A and B are on the outside.

After a non-standard rotation either A or B will be on the inside and then there are two possible cases. Firstly, if the edge is “correct” then the split face will remain touching the rotated center and the full face with color C will show on the outside.

The other case is when the edge is “incorrect”. Here the split face will be on the outside and the full color C will be touching the center.

As a rule you can now rotate the edge in the “down” direction in regards to the the rotation (where the center would be in the “up” direction) as shown here.

This way we can simulate a 3-cycle of the faces A, B and C with the 4-sided shape of the tetrahedron.

Gyro

While it isn’t necessary for a solve it is possible to reorient the whole puzzle by what’s usually called a gyro. There might be better ways to do it but here is one way that can be done in four steps.

Step 1

First you have to align the free octahedron with one of the “outer” edges. Regarding the colors it’s best to look at the colors of the adjacent octahedron. In this step you have two cases. Either the edge is already correct the you don’t have to do anything or the edge is incorrect then you have to reorient it towards the free octahedron.

Step 2

Now you have to separate one 2-layered pyramid next to the aligned free octahedron. Here you have to watch out for the three edges facing you. In case they are “incorrect” you have to reorient them towards you. Then you can move it together towards the free octahedron.

Step 3

Here you have to look at what’s left of the “upper pyramid”. The topmost piece and the “inner” piece have to be reoriented in case they are incorrect. This time the direction you have to reorient them towards is “down”, which means it’s just like you would do in a normal slice move. One handy thing is that for the “inner” piece you simply have to look on the inside by only taking these three pieces off and if you see a whole face you can just leave the piece there. If the face is 3 colored you can just take it and rotate it together with the other pieces and it will be correct.

Step 4

The last step only involves the last edge. Again, if it’s incorrect you first have to reorient it, this time towards the “down” direction. And then you take the piece and move it “over the Pyraminx”, like this, and simply put it in the right spot.

That’s all there is to the gyro and here we have all in one movement.

Comparison of Moves with MC4D

Dominik’s Pyraminx	MagicCube 4D

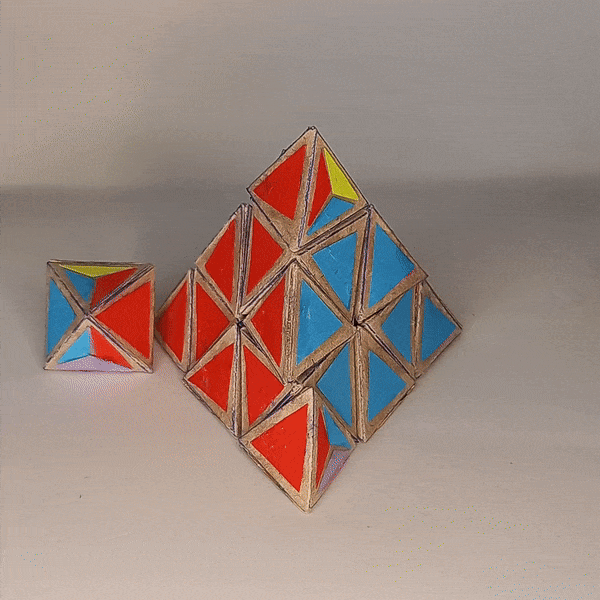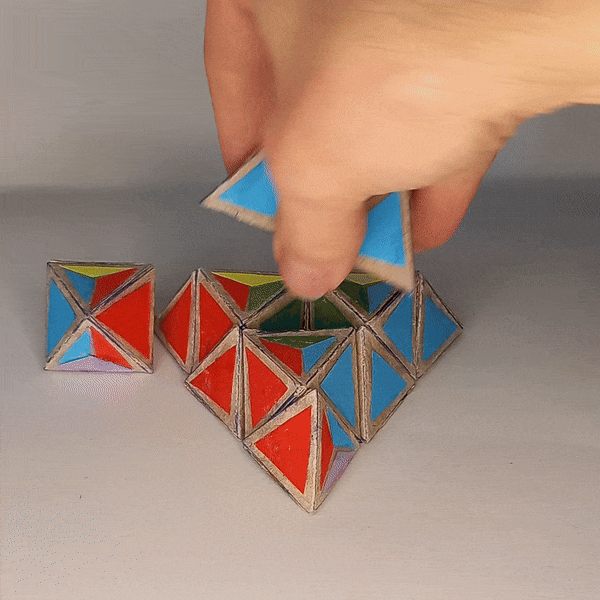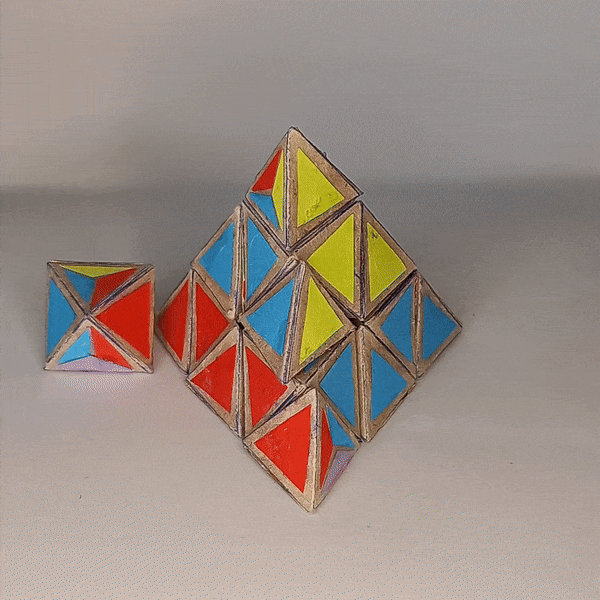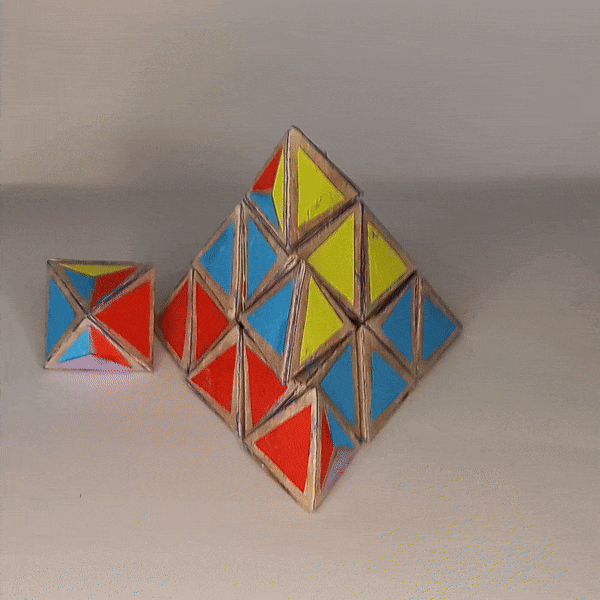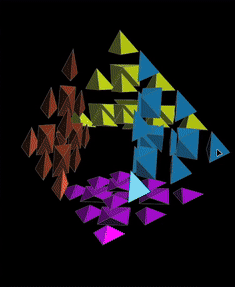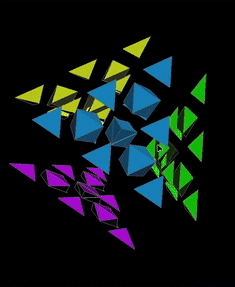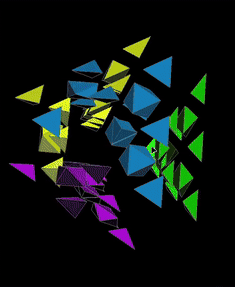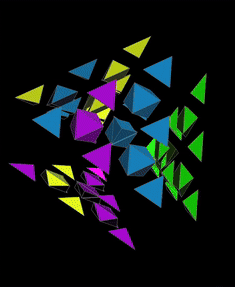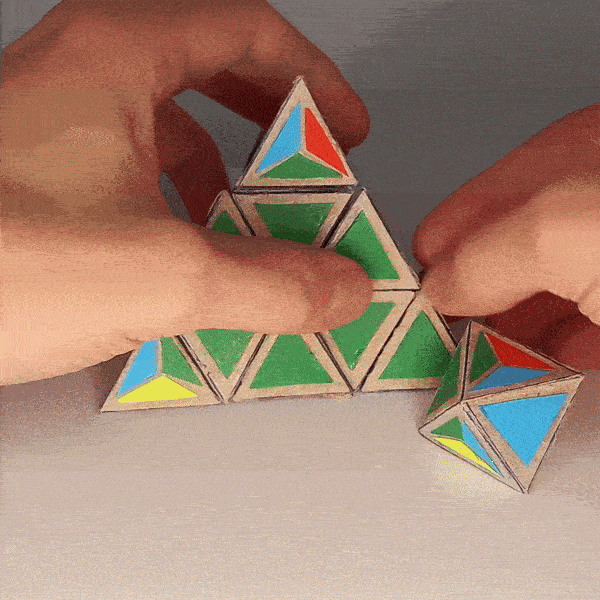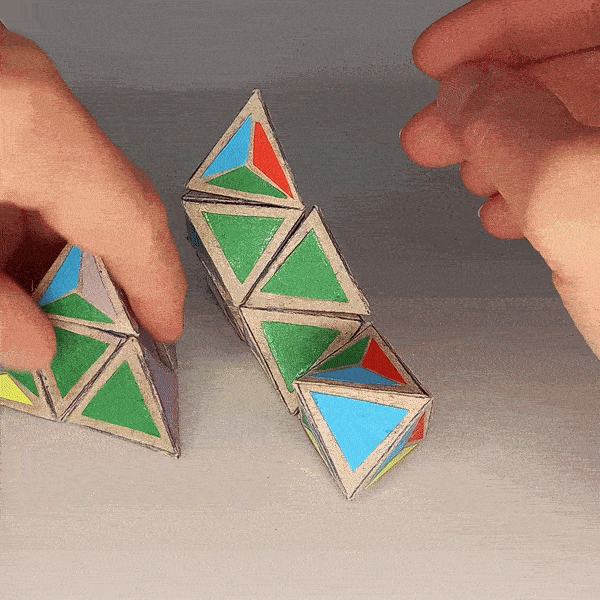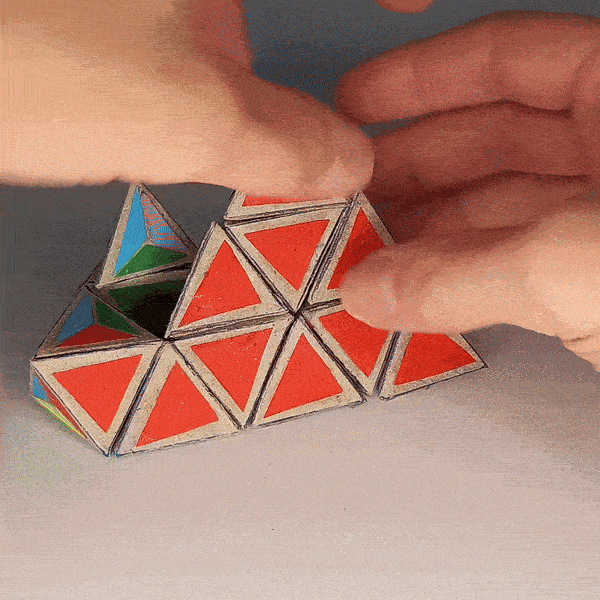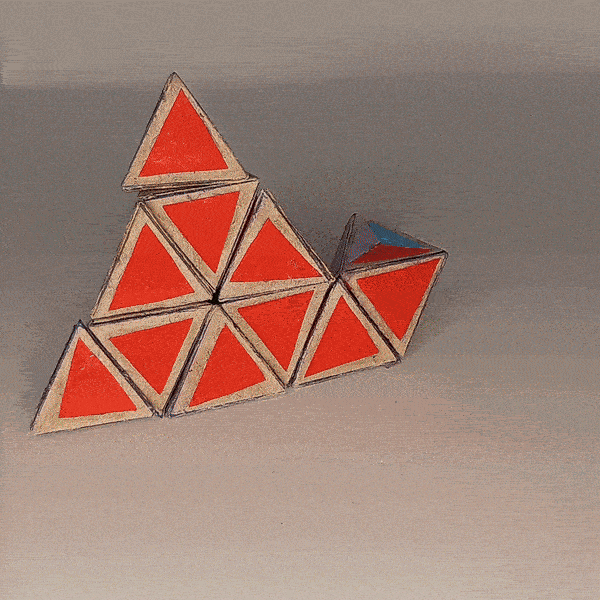Example solve

Here is a link to a video of an example scramble and solve of the puzzle:

Also you can watch a tutorial of how to solve it here:

Notes for a solve

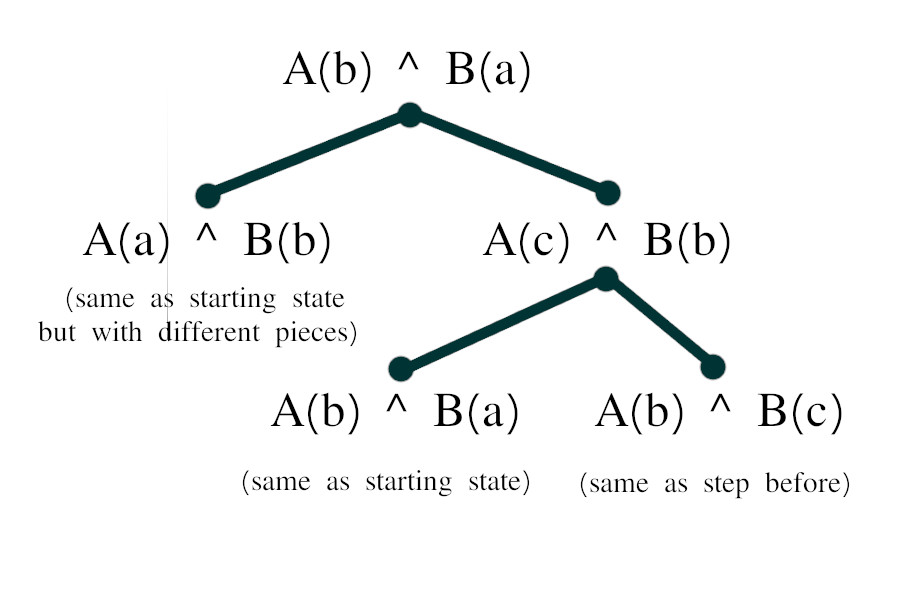
The 4D pyraminx can end up with a single edge flipped incorrectly unlike the 3D pyraminx. This state can be solved with an algorithm that flips two edges, the right slice move and an additional two edges flip. But if a piece was moved in a wrong way accidentally it can also end up in a state that’s not solvable like this. The reason for this is that there are three states that flipping an edge moves between: (a) solved state, (b) one edge correct and the other two flipped and (c) all edges incorrect.

Going from (c) to (a) requires two flips so the method above can flip edge A from (b) to (a) or (c) but then edge B will go to state (b). In the following tree diagram it can be seen how all 2 flip moves only lead to looping between unsolved states: